Lógica Proposicional - Síntese

 

Koda, o meu labrador.

 Lógica proposicional - 

Síntese

"A lógica enquanto ciência que estuda as condições de validade dos argumentos foi fundada por Aristóteles (384-322 a. C.). Paralelamente ao estudo da noção de validade e de outras noções centrais da lógica, Aristóteles desenvolveu a teoria do silogismo — um tipo de lógica dedutiva em que os elementos fundamentais são os termos e em que a validade de um argumento depende da disposição desses termos no argumento. Embora Crisipo (279-206 a. C.), um dos fundadores do estoicismo, tenha, ainda na Antiguidade, desenvolvido uma lógica em que os elementos fundamentais eram as proposições, a lógica de Aristóteles dominou esta disciplina quase incontestavelmente durante mais de dois mil e duzentos anos. A sua influência foi de tal modo grande que, no século XVIII, Kant afirmava que a lógica tinha começado e acabado com Aristóteles. No entanto, tudo isto mudaria na segunda metade do século XIX, altura em que começou um período de rápido desenvolvimento da lógica que dura até hoje. Filósofos e matemáticos como George Boole (1815-1864), Charles S. Pierce (1839-1914), Gottlob Frege (1848-1925), Bertrand Russell (1872-1970) e Kurt Gödel (1906-1978), inspirados no rigor das matemáticas, desenvolveram várias linguagens lógicas, entre elas a lógica proposicional, que vamos agora estudar".

Álvaro Nunes

In Crítica

(o sublinhado é nosso).

LÓGICA 

O que é a lógica?

A lógica proposicional é um sistema formal que se dedica à análise das proposições que constituem um argumento. 

Qual a importância  da lógica?

Através da lógica proposicional é possível avaliar a validade de um argumento. 

Em lógica proposicional aplicamos determinadas letras para substituir as proposições, tal como em aritmética substituímos números por letras: 2+3=5 pode-se exprimir por X+Y=Z quando queremos dizer qualquer número.

    

Qual a função da Lógica?

A sua função incide na verificação da validade dos argumentos (ou seja, das inferências realizadas) a partir da análise das proposições que o compõem e das operações efetuadas entre elas.

 O que é uma inferência?

A inferência é a operação mental que permite extrair uma conclusão a partir da ligação estabelecida entre as proposições anteriores (premissas).

PROPOSIÇÃO

O que é uma proposição?

A proposição é um enunciado declarativo que exprime um juízo acerca da realidade, susceptível de ser verdadeiro ou falso. 

Proposição é o que é afirmado ou negado numa frase declarativa - é o conteúdo verdadeiro ou falso de um enunciado declarativo.

Nota: 

Frase e Proposição não são sinónimos, pois duas frases declarativas diferentes podem expressar a mesma proposição.

Exemplo: "A Lola nasceu no Porto" e "O Porto é a cidade de nascimento da Lola"

 O que é uma não proposição?

Nem todas as frases que proferimos são proposições. Todas as expressões que não contenham valor de verdade não poderão ser consideradas proposições.

Interrogações/perguntas: Que horas são? Quem teve a melhor nota?

 Exclamações: Oxalá esteja bom tempo! Espero que goste!

 Pedidos;Dá-me um abraço.

 Ordens:  Fecha já a porta!

 Promessas: Prometo estudar mais. 

Orações:“Em nome do Pai e do Filho e do Espírito Santo…” 

Agradecimentos: Muito obrigada. Agradeço-te muito.

 Conselhos: Eu acho que devias pedir desculpas.

 Absurdos: Um hipopótamo voava enquanto lia livros de poesia.

 Indefinidos: Chove. Neva. Doente. Morreu. Dorme.

Serão as proposições do mesmo tipo?

As proposições poderão ser simples ou complexas.

Como se distinguem?

Simples - Proposições indivisíveis, ou seja, não se podem decompor em mais proposições. ex.: “Rodolfo come peixe”)

As proposições simples são formalizadas pelas letras P, Q, R e assim sucessivamente, denominadas de variáveis, uma vez que o seu conteúdo varia consoante a aplicação dos enunciados. 

Complexas - Proposições construídas a partir de proposições simples ligadas entre si por intermédio de operadores lógicos (ou conectivas)(enunciados compostos por 2 ou mais proposições simples articuladas entre si ex.: “Rodolfo come carne e peixe”)

 Ex.:

Koda é um labrador e é castanho

Dicionário:

P = Koda é um labrador 

Q = Koda é castanho

De acordo com esta formalização, teríamos a expressão deste modo: P e Q

PROPOSIÇÕES CATEGÓRICAS

Proposições simples e complexas

Uma proposição simples é aquela em que não estão presentes conectivas proposicionais, tais como "e", "ou", "se...então", etc. Estas proposições não podem ser decompostas em outras proposições.

Exemplo: "A Yolanda gosta de Filosofia"

Uma proposição complexa é composta por duas ou mais proposições simples ligadas através de conectivas proposicionais. As proposições complexas podem ser decompostas em proposições simples.

Exemplo: "A Yolanda gosta de Filosofia e de Biologia" 

Dentro da categoria das proposições simples encontramos as proposições categóricas. 

Proposições categóricas são aquelas que negam ou afirmam alguma coisa sobre algo (afirmam ou negam um predicado de um sujeito), sem condição ou alternativa e são precedidas por um quantificador.

    Vejam-se alguns exemplos:

• Todos os alunos são engraçados.
• Alguns alunos são engraçados.
• Nenhum aluno é engraçado.
• Alguns alunos não são engraçados. 

 FORMA CANÓNICA E FORMA LÓGICA  das proposições categóricas

FORMA CANÓNICA/Padrão	FORMA LÓGICA
Todos os alunos são interessantes	Todo S é P
Nenhum aluno é interessante	Nenhum S é P
Alguns alunos são interessantes	Algum S  é P
Alguns alunos não são interessantes	Algum S não é P

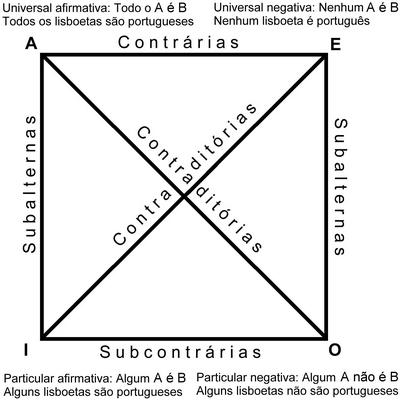
QUADRADO DA OPOSIÇÃO

Estes quatro tipos de proposições categóricas deram origem a um diagrama - o  quadrado da oposição -  que mostra as relações entre esses quatro tipos de proposições categóricas.

Quando se diz “Todos os alunos são engraçados” está a afirmar-se alguma coisa  (engraçados) sobre os alunos. 

Esta frase é precedida de um quantificador: “Todos”. 

Este tipo de proposições têm, portanto, uma qualidade e uma quantidade. A qualidade pode ser negativa ou afirmativa - podemos afirmar ou negar algo -, a quantidade pode ser universal - quando refere o conjunto de todos as coisas/indivíduos- ou particular - quando refere apenas alguns. 

Combinando estes quatro factores temos os quatro tipos de proposições categóricas estudadas pelo filósofo Aristóteles:

 Tipo A: Universal Positiva - Todo o A é B. “Todas as aves são voadoras” - Afirma-se algo sobre todas as aves.

 Tipo E: Universal Negativa - Nenhum A é B. “Nenhuma ave é voadora” - Nega-se algo sobre todas as aves (por diz-se “nenhuma”).

 Tipo I: Particular Afirmativa - Algum A é B. “Algumas pessoas são aborrecidas” - Afirma-se algo sobre uma parte do conjunto das pessoas.

Tipo O: Particular Negativa - Algum A não é B. “Algumas pessoas não são aborrecidas” - Nega-se algo sobre uma parte do conjunto das pessoas.

Nota:

O quadrado lógico não contempla as proposições singulares, como por exemplo: A Lola é apreciadora da teoria moral de Kant.

Atenção:

Nem sempre estas proposições aparecem nesta sua forma canónica. Podemos encontrar uma proposição do tipo A com esta forma: “Qualquer gato é felino”, ou uma proposição do tipo I: “Há gatos que são medrosos”, ou ainda: “Não é verdade que alguns gatos não sejam medrosos” (estamos a negar duas vezes, de modo que se trata de uma proposição do tipo I). 

É necessário estar sempre atento às expressões utilizadas e ao que elas significam -  se está a negar ou a afirmar o todo ou a parte.

MAS....

...há outros tipos de proposições que o quadrado de oposição não contempla, como é o caso das chamadas proposições singulares. As proposições singulares são aquelas que dizem respeito a um único ser ou objecto. 

Por exemplo: Portugal é um país europeu. O gato é um animal. A ESA não é uma instituição politica. (A negação destas proposições é simples.... acrescentar ou retirar um não).

NEGAÇÃO DAS PROPOSIÇÕES CATEGÓRICAS

Quadrado da oposição e negação de proposições

Como sabemos os filósofos discordam entre si e defendem, muitas vezes, teses opostas. Será então importante saber como se nega uma tese ou proposição.

Há várias maneiras de classificar proposições - pelos quantificadores (universais e particulares) e pela qualidade (afirmativas e negativas).

Se duas afirmações forem a negação uma da outra, não podem ter o mesmo valor de verdade - a verdade de uma implica a falsidade de outra e vice-versa.

Por exemplo: "Alguns livros não são agradáveis" não é a negação de "Alguns livros são agradáveis".

As relações entre os tipos de proposições categóricas.

O que mais nos interessa no quadrado da oposição é a relação de contraditoriedade. É essa a relação entre proposições que se negam umas a outras. 

Para uma proposição negar outra é necessário inverter o seu valor de verdade. Ou seja, se uma é verdadeira a outra é falsa e vice-versa. Isto acontece porque uma é o inverso da outra tanto em qualidade (negação-afirmação) como em quantidade (universal-particular).

Mas o que são proposições contrárias, subcontrárias e contraditórias?

Que relação mantêm entre si?

Tipos de relação	Descrição da relação	Implicações	Observações
Contraditoriedade (contraditórias) (A,O) e (E, I)	Duas proposições contraditórias não podem ter o mesmo valor de verdade.	A verdade de uma implica a falsidade de outra e vice-versa.	São a negação uma da outra
Contrariedade (contrárias) (A, E)	Duas proposições contrárias não podem ser ambas verdadeiras.	A verdade de uma implica a falsidade de outra, mas a falsidade de uma não implica a verdade da outra.	Podem ser ambas falsas e, por isso, não são a negação uma da outra.
Subcontrariedade (subcontrárias) (I, O)	Duas proposições subcontrárias não podem ser ambas falsas.	A falsidade de uma implica a verdade da outra, mas a verdade de uma não implica a falsidade da outra.	Podem ser ambas verdadeiras e, por isso, não são a negação uma da outra nem há entre elas uma relação de oposição.

Assim:

- A negação de "Todos os professores são altos" é "Alguns professores não são altos" ( e não "Nenhum professor é alto").

A e O têm sempre valores de verdade opostos: se A for verdadeira, O será falsa e vice-versa

- A negação de "Nenhum professor é alto" é "Alguns professores são altos".

E e I têm sempre valores de verdade opostos: se E for verdadeira, I será falsa e vice-versa;

- A negação de "Nenhum professor é alto" é "Alguns professores são altos".

A negação de uma dada proposição quantificada será uma proposição com os mesmos termos mas com diferente quantidade e qualidade. Se uma é verdadeira a outra é falsa. Qualquer proposição é inconsistente com a sua negação.

VARIÁVEIS PROPOSICIONAIS

O que são variáveis proposicionais?

Tendo em conta que a lógica formal se ocupa da forma dos argumentos, é mais fácil representar cada proposição simples com uma letra - P, Q, R, ... - (chamadas variáveis proposicionais) e as conectivas pelos seus respectivos símbolos.

São as letras que substituem as proposições.

Como traduzir as proposições complexas?

Para traduzir as proposições complexas é necessário primeiro fazer um dicionário.

Exemplo: "O João gosta de chocolate e gelado"

Dicionário: P: "O João gosta de chocolate"; Q: "O João gosta de gelado"

 Como simbolizar, por exemplo,  a expressão «e»?

Através de uma conectiva.

Expressões como «e», «mas», «ou», «se… então», «se e somente se» são alguns exemplos de conectivas justamente porque estabelecem a ligação entre as proposições.

CONECTIVAS PROPOSICIONAIS

O  que é uma conectiva (ou operador) proposicional?

As conectivas são instrumentos que permitem assegurar a relação entre as diversas proposições simples, possibilitando desta forma a construção dos nossos raciocínios.

Utilizamos conectivas proposicionais para expressar determinadas formas lógicas. Entende-se por conectiva expressões que se podem acrescentar a uma frase ou frases, formando assim novas frases:

Por exemplo: se juntarmos a expressão «ou» às frases «Platão era romano» e «Platão era grego», ficamos com a frase «Platão era romano ou Platão era grego».

Existem muitas formas conectivas: Penso que, acho que, porque...não são frases mas que servem para gerar uma frase se for colocada alguma depois dela.

Segue um quadro com a indicação das 

conectivas, sua

 leitura e respectiva simbologia.

LINGUAGEM NATURAL	CONECTIVAS PROPOSICIONAIS	SÍMBOLOS DAS CONECTIVAS
“não…” “não é verdade que…” “é falso que…”	Negação	¬
“… e …” “tanto…como…” “…, mas também…”	Conjunção	˄
“… ou…” “…a não ser que…”	Disjunção inclusiva	V
“…ou…ou…	Disjunção exclusiva	V
“Se… então…” “… desde que…” “…só se…”	Condicional	→
“…se e só se…” “… se e somente se…” “condição necessária e suficiente”	Bicondicional	↔

FORMALIZAÇÃO DE ENUNCIADOS

Como se formalizam os enunciados?

Conhecidas as conectivas, sua leitura e respetiva simbologia passemos à formalização de enunciados:

 

A.   Os labradores e os Dálmatas são cães.

           

            Dicionário:

P = Os Labradores são cães

Q = Os Dálmatas são cães

Formalização: P Λ Q

B.   A Filosofia é um saber a priori e não a posteriori.

Dicionário:

P = A Filosofia é um saber a priori.

Q = A Filosofia é um saber a posteriori

 

Formalização: P Λ ¬Q

 

C.   O dinheiro pode trazer felicidade mas também infelicidade.

                       

                        Dicionário:

P = Ter dinheiro

Q = Trazer felicidade           

 

Formalização: P → (Q Λ ¬Q)

 

NOTA:

A utilização dos parênteses revestem-se de extrema importância. Neste caso, ter dinheiro implica felicidade e  infelicidade.

Caso não existissem parênteses  P apenas implicava Q (a felicidade).

  

D. Se o ser humano é naturalmente bom, a moralidade é inata.

Existem ações más o que é o mesmo que dizer que o ser humano não é naturalmente bom,

 Logo, a moralidade não é inata. 

Dicionário:

P = O ser humano é naturalmente bom

Q = A moralidade é inata

R = Existem ações más.

Formalização: [(P → Q) Λ (R ↔ ¬P)] ∴ ¬Q

O que é uma conectiva verofuncional?

A lógica proposicional clássica lida com proposições complexas que são proposições ligadas por conectivas proposicionais - conectivas proposicionais verofuncionais.

Estas conectivas são aquelas que nos permitem aferir o valor de verdade da proposição complexa apenas sabendo o valor de verdade das proposições simples e qual a conectiva em causa.

Os operadores verofuncionais têm a propriedade de determinar o valor de verdade das frases a que dão origem e, por isso, têm um papel central na lógica proposicional. Uma conectiva proposicional é verofuncional quando o valor de verdade da proposição com a conectiva é inteiramente determinado pelo valor de verdade da proposição ou proposições sem conectiva. 

Os operadores, ou conectores, verofuncionais são: a negação, a conjunção, a disjunção  (inclusiva e exclusiva), a condicional e a bicondicional.

Um operador verofuncional é uma expressão que liga duas proposições simples e forma uma outra proposição composta. 

O operador verofuncional permite saber em que condições uma proposição composta é verdadeira ou falsa. 

Exemplo: "Vou para a Escola ou vou ao concerto". "Ou" é um operador verofuncional.

Quais são as conectivas verofuncionais?

Designação	Exemplo	Dicionário	Formalização
Proposição simples	Koda é labrador	P - Koda é labrador	P
Negação	Koda não é labrador	P - Koda é labrador	¬P
Conjunção	Koda é labrador e castanho	P - Koda é labrador Q – Koda é castanho	P˄Q
Disjunção inclusiva	Koda é labrador ou castanho	P - Koda é Labrador Q – Koda é castanho	PVQ
Disjunção inclusiva	O Koda é meu ou do Ambrósio	P - Koda é meu Q – Koda é do Ambrósio	PVQ
Condicional	Se Koda é labrador, então é castanho.	P - Koda é labrador Q – Koda é castanho	P→Q
Bicondicional	Koda é labrador se e só se for castanho	P - Koda é labrador Q – Koda é castanho.	P↔Q

 

Koda e Jim, os meus labradores.

 

As proposições podem, no entanto,  surgir com outras expressões:

 

PROPOSIÇÃO	FORMALIZAÇÂO
Koda é labrador. Não é verdade que Koda seja labrador.	¬P
Tanto Koda como oJim são labradores Quer o Koda quer o Jim são labradores O Koda é meiguinho mas o Jim  também. O Koda é meiguinhol embora o Jim   também o seja.	P˄Q
Koda é meiguinho ou agressivo Koda e Jim um deles é meiguinho (Inclui a possibilidade de as duas ser verdadeiras)	PVQ
Koda ou nasceu em Novembro ou em  Dezembro (não podem ser ambas verdadeiras)	PVQ
Se Koda é labrador, então é meiguinho. Koda é labrador se é meiguinho.	P→Q
Koda é labrador se e só se for meiguinho. Koda é labrador se e apenas se for meiguinho. Koda é labrador se for meiguinho e vice-versa.	P↔Q

Quais as funções de verdade para cada uma das conectivas proposicionais?

 

1. NEGAÇÃO

A negação inverte o valor de verdade

REGRA

A negação de uma proposição P é verdadeira, quando a proposição P for falsa e falsa se a proposição P for verdadeira.

 

P e ¬P não poderão ser simultaneamente verdadeiras, pois isso implica uma contradição.

Se P for verdadeira, ¬P é falsa e vice versa.

 

 

P	¬ P
V	F
F	V

 

 

2. CONJUNÇÃO

REGRA

A conjunção (de duas proposições P e Q) só é verdadeira se ambas as proposições simples que a constituem forem verdadeiras, sendo falsa nos restantes casos.

 A conjunção é verdadeira nas circunstâncias em que ambas

as proposições são verdadeiras

Numa conjunção, não é possível admitir um enunciado como verdadeiro existindo uma proposição constituinte falsa.

P	Q	P ∧ Q
V	V	V
V	F	F
F	V	F
F	F	F

 

  

3. DISJUNÇÃO  INCLUSIVA

REGRA

A disjunção inclusiva (entre duas proposições P e Q) é falsa quando ambas as proposições simples que a constituem são falsas, sendo verdadeira nos restantes casos.

Na disjunção inclusiva, se uma das proposições for falsa, isso não põe em causa a veracidade do enunciado, uma vez que admissão de uma poderá implicar a exclusão da outra.

 

 

A disjunção é falsa nas circunstâncias em que ambas as

proposições disjuntas são falsas

ou

é verdadeira nas circunstâncias em que pelo menos uma das

proposições que a compõem é verdadeira

 

 

P	Q	P V Q
V	V	V
V	F	V
F	V	V
F	F	F

 

 

 4.DISJUNÇÃO  EXCLUSIVA

REGRA

A disjunção exclusiva (entre duas proposições P e Q) é verdadeira quando as proposições simples que a constituem tiverem valores de verdade diferentes, sendo falsa nos restantes casos.

 

Na disjunção exclusiva, não é admissível as proposições terem valores iguais, uma vez que a admissão de uma pressupõe a exclusão da outra.

 

Uma disjunção exclusiva é verdadeira

quando apenas um dos seus componentes o for.

 

P	Q	P V Q
V	V	F
V	F	V
F	V	V
F	F	F

 

5.  CONDICIONAL

 Regra:

A condicional é falsa nas circunstâncias em que a proposição antecedente

é verdadeira e a proposição consequente é falsa

P	Q	P → Q
V	V	V
V	F	F
F	V	V
F	F	V

 

 

 

6.  BICONDICIONAL («se e só se», «é o mesmo que», «equivalente a»)

A bicondicional é verdadeira nas 

circunstâncias em que  as 

proposições que a compõem são ambas

falsas ou ambas verdadeiras

 

A bicondicional ou equivalência material ou é a conectiva proposicional que une duas proposições simples P e Q, dando origem a uma nova proposição P ↔ Q, traduzindo as expressões «se e só se», «é o mesmo que», «equivalente a» da linguagem natural.

 

EXEMPLOS

O conhecimento é verdadeiro    se e só se    for demonstrado.

Preocupar-se com os outros equivale a ser altruísta.

P ↔ Q

P	Q	P ↔ Q
V	V	V
V	F	F
F	V	F
F	F	V

\

Assim.....

TABELA DE VERDADE

                                                                                

Prop 1	Prop 2	Neg.   ~	Conjunção   Λ	Disjunção inclusiva V	Disjunção exclusiva V	Condicional  →	Bicondicional ⇄
P	Q	Não	e	Ou	Ou…ou	Se…então	Se e somente   se …
V	V		V	V	F	V	V
V	F		F	V	V	F	F
F	V		F	V	V	V	F
F	F		F	F	F	V	V

10ºA

FORMALIZAÇÃO DE ENUNCIADOS

Formalização lógica das proposições.

Formalização/ tradução para linguagem formal: P ∧ Q

Para fazer o dicionário utilizamos as letras para simbolizar apenas as proposições simples. É preciso ter atenção à negação: não esquecer que é uma conectiva - por isso a seguinte proposição: "O João não gosta de gelado" traduz-se da seguinte maneira:

Dicionário: P: "O João gosta de gelado"

Formalização/tradução para linguagem formal:  ~P

Este tipo de linguagem permite formalizar proposições com várias variáveis e várias conectivas. 

Nós só iremos traduzir proposições até três variáveis (três letras P, Q, R).

Como se formalizam os enunciados?

Conhecidas as conectivas, sua leitura e respectiva simbologia passemos à formalização de enunciados:

A.   As laranjas e o limões são frutos.

          

            Dicionário:

P = As laranjas são frutos.

Q = Os limões são frutos.

 

Formalização: P Λ Q

B.   B. O conhecimento provém da experiência e não da razão.

Dicionário:

P = O conhecimento provém da experiência.

Q = O conhecimento provém da razão.

 

Formalização: P Λ ¬Q

 

C. As laranjas podem trazer doçura ou não doçura

                       

 Dicionário:

P = Comer laranjas

Q = Trazer doçura          

 

Formalização: P → (Q Λ ¬Q)

 

D. Vamos formalizar agora um argumento: 

Se o ser humano é naturalmente bom a moralidade é inata.

Existem ações más é o mesmo que dizer que o ser humano não é naturalmente bom,

 Logo, a moralidade não é inata.

 

Dicionário:

P = O ser humano é naturalmente bom

Q = A moralidade é inata

R = Existem ações más

 

Formalização:

 [(P → Q) Λ (R ↔ ¬P)] ∴ ¬Q

 

NOTA:

A utilização dos parênteses revestem-se de extrema importância. Neste caso, ter dinheiro implica felicidade e  infelicidade.

Caso não existissem parênteses  P apenas implicava Q (a felicidade).

 

Conectivas proposicionais e parênteses

Cada conectiva proposicional binária terá parênteses.

Exemplo:

O Afonso toca guitarra  e o João  vai andar de mota.

P – O Afonso toca guitarra

Q – O João vai andar de mota.

 (P Ʌ Q)

 

Apenas a negação não apresenta parênteses

 

Exemplo:

 

O Afonso não toca guitarra

 

 ¬ P

O âmbito das conectivas proposicionais consiste na parte da fórmula sobre a qual as conectivas operam.

 

Por exemplo:

Na fórmula P e não Q a negação aplica-se apenas à variável proposicional Q, enquanto a conjunção se aplica a toda a fórmula. Daí, a conjunção ser a conectiva com maior âmbito.

 

A conectiva principal ou com maior âmbito é a que se aplica a toda a proposição.

 

Exemplo:

Não é verdade que o Afonso toca guitarra  e o João vai andar de mota.

¬ (P Ʌ Q)

Se o Afonso toca guitarra e o João vai andar de mota, então não há teste de Filosofia

 

((P Ʌ Q) → ¬ R)

 

Como e quando se colocam os parênteses  nas proposições complexas?

Os parêntesis usam-se sempre que é necessário isolar uma conectiva dominante, para se “dar força” (âmbito da conectiva) a uma conectiva de menor dominância. 

Ordem decrescente de dominância das conectivas:

Bicondicional, 

Condicional, 

Conjunção, 

Disjunção 

Negação. 

 

Ser dominante significa que a conectiva resiste na expressão, até as outras terem sido avaliadas quanto ao seu valor de verdade. 

Ou seja, a dominante é a última a ser avaliada.

 

Conectivas com maior e menor âmbito

Neste tipo de casos é necessário ter em atenção qual a conectiva com maior âmbito. Para isso utilizamos parêntesis. 

Exemplo: P ⟶ (Q ν R)

Aqui a conectiva de maior âmbito é a condicional. Isto é, é a conectiva principal desta proposição. Devemos resolver primeiro as que têm menor âmbito e só depois as de maior âmbito.

Tal como na matemática, é aquela operação que vamos "resolver" em último lugar de modo a dar-nos o "resultado final".

Dominância máxima (maior âmbito) e Dominância mínima (menor âmbito)

Ordem crescente de dominância das conectivas:  

negação, disjunção, conjunção, condicional e bicondicional

Negação ~ + 

Disjunção ∨ ++ 

Conjunção ∧ +++ 

Condicional → ++++

Bicondicional ↔++++++ 

 

Conectiva principal de uma fórmula.

Esta aplica-se a toda a fórmula, de modo que na construção de tabelas de verdade com mais do que uma conectiva, avança-se das conectivas de menor âmbito para as de maior âmbito, sendo que o resultado final da tabela surge na conectiva principal (a última operação a efectuar). 

 

Conectiva Dominante	Exemplo	Dicionário	Formalização
Negação e condicional	Não é verdade que,  se a Ana estuda, tem boa nota no teste	P – A Ana estuda Q – A Ana tem boa nota no teste.	~ (P → Q)
Condicional e negação	Se a Ana estuda, não terá problemas	P – A Ana estuda Q – A Ana terá problemas	P →~ Q
Conjunção e conjunção	A Ana estuda, é atenta e é bonita	P – A Ana estuda Q – A Ana é atenta R – A Ana é bonita	P ∧Q∧R
Conjunção, condicional e negação	A Ana estuda e, se estiver com atenção, não terá problemas com o teste.	P – A Ana estuda Q – A Ana está com atenção R – A Ana tem Problemas com o teste.	P∧(Q→~R)
Bicondicional, conjunção e negação	A Ana estuda se e só se estiver com atenção e não tiver problemas.	P – A Ana estuda Q – A Ana está com atenção R – A Ana tem problemas.	P ↔(Q∧~R)
Disjunção, conjunção  e condicional	A Ana estuda muito ou tem talento e, se tiver sorte, terá sucesso.	P – A Ana estuda muito Q – A Ana tem talento R – A Ana tem Sorte S – A Ana tem sucesso	(P ∨Q) ∧ (R→S)

O que é uma tabela de verdade?

Uma tabela de verdade é um dispositivo gráfico que permite exibir as condições de verdade de uma forma proposicional dada. O método das tabelas de verdade permite-nos determinar as condições de verdade de uma dada proposição. Isto é, as tabelas de verdade permitem-nos calcular em que condições uma proposição complexa é verdadeira ou falsa quando não sabemos o valor de verdade das proposições simples que a constituem.

Como se constrói uma tabela de verdade?

De uma maneira geral, a ordem com que se fazem as operações numa tabela de verdade é sempre a mesma: dos operadores de menor âmbito para os operadores de maior âmbito. 

 

Para determinar se um argumento é válido, segundo o método das tabelas de verdade , procede-se aos seguintes passos :

 

·   Elabora-se o dicionário, atribuindo uma letra proposicional/variável de fórmula (ex.: p, q, r, s …) a cada proposição simples;

·         Formaliza-se o argumento ( tradução em linguagem simbólica : variáveis ordenadas segundo a sequência, as conectivas que as articulam e os parêntesis curvos ou rectos quando necessário);

·         Constrói-se a   tabela operacionalizando as conectivas lógicas desde as de menor âmbito ou dominância até às de maior âmbito (que expressará o resultado da tabela);

·         A elaboração da tabela segue o mesmo procedimento  da elaboração das tabelas de verdade de cada uma das conectivas.

 

Como construir uma tabela de verdade?

 

 - Numa tabela de verdade deverão constar em cada coluna quatro espaços ocupados por valores lógicos: as proposições serem ambas verdadeiras, serem ambas falsas, ou ser uma verdadeira e a outra falsa.

- Na tabela o número de espaços em cada coluna depende do número de variáveis e há uma fórmula para o calcular: 2 elevado a 2 - 4 espaços.

 

P	Q
V	V
V	F
F	V
F	F

 

- Se tivermos três variáveis (P, Q e R) temos 2 elevado a 3 - 8 espaços.

 

P	Q	R
V	V	V
V	V	F
V	F	V
V	F	F
F	V	V
F	V	F
F	F	V
F	F	F

 

 

EXEMPLO:

 

Como calcular, recorrendo a uma tabela de verdade, os valores da seguinte fórmula? 

~ (P ∧ ~Q)→R

 

(Não é verdade que o Afonso toca guitarra e o João não anda de mota se há teste de Filosofia).

 

 10º B

1º Passo: Nas três primeiras colunas colocar as variáveis P, Q e R

P	Q	R
V	V	V
V	V	F
V	F	V
V	F	F
F	V	V
F	V	F
F	F	V
F	F	F

2º Passo: Na quarta coluna colocar ~Q ( como ~P e ~R não constam da fórmula, não é necessário colocar os seus valores na tabela).

P	Q	R	~Q
V	V	V	F
V	V	F	F
V	F	V	V
V	F	F	V
F	V	V	F
F	V	F	F
F	F	V	V
F	F	F	V

 

 

3º Passo: Na quinta coluna ficará a conjunção que está entre parênteses (P ∧~Q), pois já temos atrás os valores de P e de ~Q indispensáveis para calcular esta  conjunção.

P	Q	R	~Q	(P ∧~Q)
V	V	V	F	F
V	V	F	F	F
V	F	V	V	V
V	F	F	V	V
F	V	V	F	F
F	V	F	F	F
F	F	V	V	F
F	F	F	V	F

 

4º Passo: Na sexta coluna teremos de fazer a negação do parênteses anterior, ou seja, calcular os valores de ~(P ∧~Q)

P	Q	R	~Q	(P ∧~Q)	~(P∧~Q)
V	V	V	F	F	V
V	V	F	F	F	V
V	F	V	V	V	F
V	F	F	V	V	F
F	V	V	F	F	V
F	V	F	F	F	V
F	F	V	V	F	V
F	F	F	V	F	V

 

5º Passo: Por fim, na sétima coluna, colocamos a fórmula completa  ~ (P ∧ ~Q)→R, pois já temos atrás os valores necessários para colocar os respectivos valores lógicos. neste caso já temos o antecedente ~(P∧~Q) e o consequente R.

 

P	Q	R	~Q	(P ∧~Q)	~(P∧~Q)	~ (P ∧ ~Q)→R
V	V	V	F	F	V	V
V	V	F	F	F	V	F
V	F	V	V	V	F	V
V	F	F	V	V	F	V
F	V	V	F	F	V	V
F	V	F	F	F	V	F
F	F	V	V	F	V	V
F	F	F	V	F	V	F

 10ºC

TAREFA:

 Como calcular, recorrendo a uma tabela de verdade, os valores da seguinte fórmula?

Caso o Afonso  tenha razão, não há guitarristas originais; e se não há guitarristas originais, a música  é imitação.

1.  Fazemos o o dicionário:

P = Afonso  tem razão.
   Q = Há guitarristas originais 
   R = A música é imitação.

10ºA

2.  Faz-se a formalização. 

Podemos proceder por passos sucessivos, de modo a termos uma maior garantia de não cometer erros. Assim, num primeiro momento, podemos substituir apenas as proposições simples pelas respetivas variáveis proposicionais:

Caso P,  não Q; e se  não Q → R

 

E só depois proceder à formalização completa (note-se que ‘Caso P, não Q’ é o mesmo que ‘Se P, então ¬ Q’):

(P → ¬Q) ∧ (¬Q → R)

Para facilitar o nosso trabalho podemos considerar que estamos perante duas proposições, P → ¬Q e ¬Q → R, ligadas pelo operador conjunção. 

 

A. Calculamos primeiro os valores de verdade para P → ¬Q 

 

B. Depois para ¬Q → R. 

 

C. Calculamos, por fim,  os valores para a conjunção, ficando a saber os valores de verdade possíveis para a proposição.

P	Q	R	(P	→	¬Q)	∧	(¬Q	→	R)
V	V	V	V	F	F	F	F	V	V
V	V	F	V	F	F	F	F	V	F
V	F	V	V	V	V	V	V	V	V
V	F	F	V	V	V	F	V	F	F
F	V	V	F	V	F	V	F	V	V
F	V	F	F	V	F	V	F	V	F
F	F	V	F	V	V	V	V	V	V
F	F	F	F	V	V	F	V	F	F

 

Alguns exercícios:

. Construa a tabela de verdade das seguintes proposições complexas:

A COMPLETAR

 ARGUMENTOS

 

 O que é um argumento?

Argumento é uma sequência de proposições organizadas de tal modo que a conclusão a que chegamos tem por base outra ou outras proposições a que chamamos premissas. 

Exemplo: 

Todos os homens são mortais. 

Sócrates é um homem. 

Logo, Sócrates é mortal.

Argumentos na forma padrão

Nem sempre os argumentos se nos apresentam na forma canónica. Veja o seguinte exemplo:

Lia - Acho que as touradas não deviam ser permitidas.

Lua - Porquê?

Lia - Nas touradas os animais são tratados cruelmente. Ora, a crueldade para com os animais não devia ser permitida.

Lua - Julgo que entendi o teu raciocínio.

É capaz de colocar este argumento na forma canónica?

O que é a forma canónica?

Forma padrão ou forma canónica: modo estabelecido para apresentar o argumento, enunciando primeiro as premissas e a seguir a conclusão.

A. Enunciar a conclusão em primeiro lugar

“O ensino deve privilegiar o desenvolvimento de competências, uma vez que, hoje em dia, o conhecimento está disponível on-line e os cidadãos só precisam de saber procurá-lo, seleccioná-lo e fazer a sua apropriação pessoal”

Forma canónica ou padrão

Premissas:

O conhecimento está disponível on-line.

Os cidadãos só precisam de saber procurar, seleccionar e fazer a sua apropriação.

Conclusão:    

Logo, o ensino deve privilegiar o desenvolvimento de competências.

B. Enunciar a conclusão entre as premissas

“ A minha irmã adora cinema, por isso tenho a certeza de que vai gostar do Matrix, dado que não há apreciador de cinema que não goste do Matrix”.

Forma canónica ou padrão

Premissas:

Todos os apreciadores de cinema gostam do Matrix.

A minha irmã adora cinema.

Conclusão:

Logo, a minha irmã vai gostar do Matrix

Validade dos Argumentos

 Como se determina a validade de um argumento?

A lógica analisa as inferências do ponto de vista formal no sentido de verificar a validade dos argumentos - tabelas de verdade e inspetores de circunstancias.

Podemos verificar a validade dos enunciados através das tabelas de verdade utilizando dois métodos:

         1. Tabelas de verdade

        2. Inspector de circunstâncias

Enquanto o primeiro se pode aplicar a todos os enunciados, o segundo apenas aos enunciados argumentativos.

1. TABELAS DE VERDADE

(VER ACIMA) ... 

2. INSPECTOR DE CIRCUNSTÂNCIAS

O que são inspectores de circunstâncias?

Um inspector de circunstância, com o recurso às tabelas da verdade, pode revelar se um argumento é válido pela simples constatação da presença ou não de circunstâncias que possuem premissas verdadeiras e conclusão falsa.

São modelos gráficos ao qual se recorre para aferir a validade dedutiva de um argumento. É um tipo de tabela de verdade, ou de validade, para argumentos em que se apresentam todas as circunstancias em que as premissas e a conclusão que compõem o argumento são verdadeiras ou falsas. Cada uma das linhas da tabela ilustra um desses exemplos.

 Um inspector de circunstância, com o recurso às tabelas da verdade, pode revelar se um argumento é válido pela simples constatação da presença ou não de circunstâncias que possuem premissas verdadeiras e conclusão falsa.

EXEMPLO:

 

Teste a  validade das seguinte forma argumentativa através de um Inspetor de circunstância. 

A. Se estiver  sol e não chover, vou à praia

Está sol e não chove 

Logo, vou à praia.

 

Dicionário:

P - Se estiver  sol 

Q- Chover

R- Vou à praia 

 

Formalização:

 

(P˄¬Q)→R

(P˄¬Q)

∴R

 

Construção do inspetor de circunstancias:

Para construir a tabela do inspetor de circunstâncias deste argumento, precisamos de colocar as variáveis proposicionais (P, Q e R) e depois mais três colunas: duas para as premissas e uma para conclusão antecedida pelo símbolo ∴

Na tabela do inspetor de circunstâncias, não vamos calcular o valor da formula final, mas antes de cada uma das premissa e a respetiva conclusão.

Em cada coluna vamos realizar os cálculos lógicos necessários até atingirmos os valores da fórmula proposicional que constitui cada premissa e a conclusão. Neste caso, a conclusão é o mais fácil, pois consiste apenas na variável R e, assim, basta repetir os valores de R.

P	Q	R	(P˄             ¬Q)         →R			(P˄¬Q)	∴R
V	V	V	F	F	V	F	V
V	V	F	F	F	V	F	F
V	F	V	V	V	V	V	V
V	F	F	V	V	F	V	F
F	V	V	F	F	V	F	V
F	V	F	F	F	V	F	F
F	F	V	F	V	V	F	V
F	F	F	F	V	V	F	F
1º Lugar			4º Lugar *	3º Lugar	5º Lugar	6º Lugar *	2º Lugar

Verificar a validade do argumento

 

Este argumento é válido pois, como notamos na 3ª linha, as premissas são ambas verdadeiras e a conclusão também é verdadeira.

 

NOTA:

A dedução da validade de um argumento deve ser justificada pelo facto de, na tabela do inspetor de circunstâncias, não se verificar qualquer caso em que as premissas sejam verdadeiras e a conclusão falsa.

 B - Um outro exemplo:

B. Se estudar lógica, vou ter boa nota na ficha de avaliação

Se tiver boa nota na ficha de avaliação, tenho boa nota no semestre 

Logo, tenho boa nota no semestre se e só se estudar lógica.

Dicionário:

P - Estudar lógica

Q- Ter boa nota na ficha de avaliação

R- Ter boa nota no semestre

Formalização:

 (P→Q)

Q→R

∴(R↔P)

Construção do inspetor de circunstancias:

P	Q	R	P→Q	Q→R	∴R↔P
V	V	V	V	V	V
V	V	F	V	F	F
V	F	V	F	V	V
V	F	F	F	V	F
F	V	V	V	V	F
F	V	F	V	F	V
F	F	V	V	V	F
F	F	F	V	V	V

C - Um outro exemplo: 

Se os impostos forem elevados, o poder de compra dos cidadãos é reduzido. 

Um estudo verificou que o poder de compra dos cidadãos é reduzido.

Os impostos são elevados.

Dicionário:

P = os impostos «são» elevados

Q = o poder de compra dos cidadãos é reduzido

Formalização:

Verifiquemos, então, a validade do argumento a partir do método das tabelas de verdade.

P	Q	P →Q	Q	∴ P
V	V	V
V	F	F
F	F	V
F	V	V

 

PASSO 1.

Construir a tabela com as 2 colunas das 2 variáveis presentes no enunciado (P e Q) e 4 linhas que correspondem às combinações possíveis e condições e verdade entre essas 2 variáveis.

 

  

PASSO 2.

Determinar o resultado lógico da implicação (condicional) entre P e Q.

V

F

V

V

 

 

PASSO 3.

Determinar o resultado lógico da conjunção entre P → Q        e Q       .

 

 

 

PASSO 4.

Determinar o resultado lógico da implicação entre o resultado da conjunção entre a primeira e segunda premissa             e P               

 

CONCLUSÃO

Apesar de eventualmente as premissas e conclusão serem verdadeiras, o argumento é inválido porque não podemos inferir objetiva e formalmente que os impostos são elevados com base nas premissas anteriores.

A causa de se verificar que o poder de compra dos cidadãos é reduzido, não permite concluir (com base nas premissas) que, inequivocamente, os impostos são elevados.

 

INSPETOR DE CIRCUNSTÂNCIAS

Este sistema de verificação da validade recorre às tabelas de verdade enquanto estrutura,  no entanto a sua aplicação é distinta, uma vez que a operação não incide propriamente nas conectivas do enunciado, mas antes nas premissas que constituem o argumento.

Consideremos um outro exemplo, agora ligeiramente mais complexo:

 

Exemplo:

Agimos por vontade ou necessidade. Se agirmos por necessidade não existe livre arbítrio. Se agimos por vontade existe livre-arbítrio. Agimos por vontade, portanto existe livre-arbítrio

 

Dicionário:

P  = Agir por vontade

Q = Agir por necessidade

R  = Existe livre-arbítrio

 

Formalização:

Agimos por vontade ou necessidade.    P V Q

Se agirmos por necessidade não existe livre arbítrio.     Q → ¬R

Se agirmos por vontade existe livre-arbítrio.     P → R  

Agimos por vontade.   P

 Existe livre-arbítrio.      R

 

 

Fórmula lógica do argumento:

P V Q,  Q → ¬R,  P → R   ∴ R  

  Será este argumento válido?

 

 

P	Q	R	P V Q	Q → ¬R	P → R	∴ R

PASSO 1.

Resultado lógico da disjunção inclusiva  entre P e Q (1)

              

PASSO 2.

Resultado lógico da implicação entre Q e ¬R (  2 )

 

PASSO 3.

Resultado lógico da implicação entre P e R (    3)

 

PASSO 4.

Valores de P ( 4 )

 

PASSO 5.

Valores de R (CONCL.)

 

 

 

 

RESULTADO

Um argumento é dedutivamente válido quando se verificar em pelo menos uma circunstância (linha) as premissas e conclusão serem verdadeiras  e não existir numa outra situação de premissas verdadeiras e conclusão falsa.

Portanto este argumento (3ª linha) é válido.

 

 

O seguinte exemplo descreve a situação de um argumento inválido

 

A lógica é um exercício mental ou complicado.

A lógica é um exercício mental.

Então, é um exercício complicado.

 

 FORMAS ARGUMENTATIVAS VÀLIDAS

NEGAÇÃO DUPLA De uma fórmula com negação dupla podemos inferir uma afirmação	¬¬ P ∴ P
MODUS PONENS Afirma o antecedente ∴ Afirma a consequente	(P → Q) P ∴   Q
MODUS TOLLENS Nega a consequente ∴ Nega a antecedente	(P → Q) ¬Q ∴ ¬P

 

1ª LEI DE MORGAN A negação da conjunção “P e Q” é igual à disjunção “não P e não Q”.	¬ (P ∧ Q) ∴ (¬P V ¬Q)
2ª LEI DE MORGAN A negação da disjunção “P ou Q” é igual à conjunção “não P e não Q”	¬ (P V Q) ∴ (¬P ∧ ¬Q)

 

SILOGISMO HIPOTÉTICO	(P → Q) (Q → R) ∴ (P → R)
SILOGISMO DISJUNTIVO	(P V Q) ¬P ∴ Q

 

CONTRAPOSIÇÃO

(P → Q) ∴ (¬Q → ¬P)

PRINCIPAIS FALÁCIAS FORMAIS

As falácias formais são a expressão de raciocínios inválidos, porque infringem uma ou mais regras lógicas. Estes tipos de erros não são fáceis de identificar, pois assentam na estrutura do argumento e não na verdade/falsidade da conclusão.

 

A lógica proposicional apresenta dois tipos de falácias muito comuns na realização das inferências, na medida em que as suas fórmulas se assemelham às regras tautológicas do modus ponens e modus tollens. 

Essas falácias denominam-se por afirmação do consequente e negação do antecedente.

 

FALÁCIA DA AFIRMAÇÃO DO CONSEQUENTE

Esta falácia apresenta um tipo de raciocínio muito semelhante à regra do modus ponens. No entanto, o erro formal cometido consiste em deduzir o antecedente a partir da afirmação do consequente, tornando-o inválido.

É o que acontece no seguinte exemplo:

 

Se comer doces os níveis de colesterol vão aumentar.

Como os níveis de colesterol aumentaram

Então comi doces.

P → Q

Q

∴ P

 

O raciocínio está formalmente incorreto, pois não temos garantias de que os níveis de colesterol aumentaram (consequente) devido ao facto de termos comido doces (antecedente), uma vez que poderiam existir outras causas.

Podemos deduzir que se comermos doces os níveis de colesterol vão aumentar (modus ponens), mas não o contrário.

 

FALÁCIA DA NEGAÇÃO DO ANTECEDENTE

Esta falácia apresenta um tipo de raciocínio muito semelhante à regra do modus tollens. No entanto, o erro formal cometido consiste em deduzir o consequente a partir da negação do antecedente, tornando por isso o argumento também inválido.

Vejamos este argumento a partir do exemplo anterior:

 

Se comer doces, os níveis de colesterol vão aumentar.

Como não comi doces,

então os níveis de colesterol não vão aumentar.

 

P → Q

¬P

∴ ¬Q

 

O raciocínio está formalmente incorreto, pois não temos garantias de que os níveis de colesterol aumentaram (consequente) devido ao facto de termos comido doces (antecedente), uma vez que poderiam existir outras causas.

Podemos deduzir que se comermos doces os níveis de colesterol vão aumentar (modus ponens), mas não o contrário.

  

Segue aqui um quadro comparativo entre as falácias de afirmação do consequente e negação do antecedente e as formas válidas modus ponens e modus tollens, para estabelecer as suas diferenças e semelhanças.

 

 

 

 Lola