Quadrado de oposição

Quadrado de oposição

Diagrama que ilustra as diversas relações lógicas entre as quatro formas lógicas da lógica aristotélica:

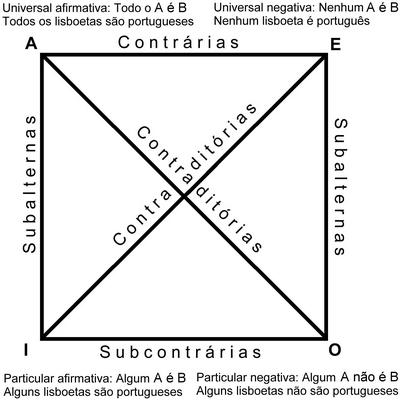
Assim, entre as formas lógicas A e I, por um lado, e E e O, por outro, há uma relação de subalternidade: A implica I, e E implica O. Esta relação é falsa, a menos que se excluam classes vazias; mas sem ela a lógica aristotélica cai por terra. 
De modo que é necessário excluir todas as proposições que falsificam a relação de subalternidade. Para isso, exclui-se todas as proposições que se refiram a classes vazias (classes como “lobisomens”, que não têm elementos). 
Com base na mesma exclusão de classes vazias é possível afirmar que as formas

1. A e E são contrárias, isto é, que não podem ser ambas verdadeiras, mas podem ser ambas falsas;
2. I e O são subcontrárias, isto é, que não podem ser ambas falsas, mas podem ser ambas verdadeiras. A única relação do quadrado que não depende da exclusão de classes vazias é a de contraditoriedade ou negação, que existe entre
3. A e O, por um lado, e entre E e I, por outro. Isto significa que A e O têm sempre valores de verdade opostos: se A for verdadeira, O será falsa e vice-versa; se E for verdadeira, I será falsa, e vice-versa. 

O diagrama é ainda hoje útil para ilustrar a negação correcta de proposições universais. 

Murcho, Desidério, O Lugar da Lógica na Filosofia,  

cap. 6 (Lisboa: Plátano, 2003).

                                           Lola