Condicional e Bicondicional

Condicional e Bicondicional

O conectivo "se… então…" 

 A condicional

condicional | adj. 2 g. | s. m.

con·di·ci·o·nal
(latim conditionalis, -e)

adjectivo de dois géneros

1. Que exprime condição.

2. Dependente de condição.

3. Diz-se do modo que põe a ideia do verbo subordinada a condição.

substantivo masculino

4. Esse modo verbal.

"condicional", in Dicionário Priberam da Língua Portuguesa [em linha], 2008-2013, https://www.priberam.pt/dlpo/condicional [consultado em 22-11-2017].

A condicional se p então q é outra proposição que tem como valor lógico F se p é verdadeira e q é falsa. O símbolo p → q representa a condicional, com a seguinte tabela-verdade: 

Exemplo:

P: 7 + 2 = 9
Q: 9 – 7 = 2
p → q: Se 7 + 2 = 9 então 9 – 7 = 2 

p = 7 + 5 < 4
q = 2 é um número primo
p → q: Se 7 + 5 < 4 então 2 é um número primo. 

p = 24 é múltiplo de 3
q = 3 é par
p → q: Se 24 é múltiplo de 3 então 3 é par. 

p = 25 é múltiplo de 2
q = 12 < 3
p → q: Se 25 é múltiplo de 2 então 2 < 3. 

O conectivo "se e somente se" 

A bicondicional

bicondicional

  

adj. lóg. Operador de la lógica proposicional que significa «si y solo si...».

Diccionario Enciclopédico Vox 1. © 2009 Larousse Editorial, S.L.

A bicondicional p se e somente se q é outra proposição que tem como valor lógico V se p e q forem ambas verdadeiras ou ambas falsas, e F nos outros casos. 

O símbolo    representa a bicondicional, com a seguinte tabela-verdade: 

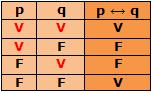
Exemplo

p = 24 é múltiplo de 3
q = 6 é ímpar
 = 24 é múltiplo de 3 se, e somente se, 6 é ímpar. 

p = 25 é quadrado perfeito
q = 8 > 3
= 25 é quadrado perfeito se, e somente se, 8 > 3

p = 27 é par
q = 6 é primo
= 27 é par se, e somente se, 6 é primo 

introdução bicondicional

Introdução_Bicondicional permite inferir que, se B se segue a partir de A, e A Decorre B, então A Se_e_somente_se B. Por exemplo, a partir das declarações "se eu estou respirando, então eu estou vivo" e "se eu estou vivo, então eu estou respirando", pode-se inferir que "eu estou respirando, se e somente se eu estiver vivo "ou, igualmente inferível:" Eu estou vivo, se e somente se eu estou respirando. "

Na interpretação proposicional, a ⇔ b significa que a implica b e b implica a; em outras palavras, que as proposições são equivalentes, o que é dizer, ambas são verdadeiras ou falsas ao mesmo tempo. Isso não significa que elas tem o mesmo significado. Exemplo: "O triângulo ABC tem dois lados iguais", e "O triângulo ABC tem 2 ângulos iguais". O antecedente é a premissa ou a causa e o consequente é a consequência. Quando uma implicação é traduzida por um julgamento hipotético (ou condicional) O antecedente é chamado de "hipótese (ou de condição) e o consequente é chamado de tese.

Uma forma comum de se demonstrar um bicondicional é usar sua equivalência para a conjunção de duas condicionais ,em que há uma troca entre a hipótese e a conclusão, demonstrando-as separadamente.

                                            Lola