Argumentos: Validade
Depois de se aprender a usar tabelas de verdade para determinar se uma dada proposição é verdadeira ou falsa, pode-se dar o passo seguinte e usar as tabelas de verdade para determinar também se certos argumentos são válidos ou inválidos.
Usar tabelas de verdade para testar a validade de argumentos.
Como construir sequências de tabelas de verdade para argumentos?
Ao construir tabelas de verdade o que se faz é calcular, de acordo com o funcionamento das cinco conectivas, os valores de verdade (V e F) que se coloca nos respetivos espaços a isso destinados. A última coluna a ser preenchida diz-nos em que condições a proposição representada é verdadeira ou é falsa. Até aqui estamos apenas a falar de proposições.
Mas como passar das proposições para os argumentos? A explicação é simples: os argumentos são formados por premissas e conclusão, que são, por sua vez, proposições; além disso, sabemos que os argumentos válidos não podem ter, ao mesmo tempo, premissas todas verdadeiras e conclusão falsa. Assim, ao colocarmos lado a lado as tabelas de verdade para cada premissa e para a conclusão (fazendo uma sequência de tabelas ligadas, em que se começa pelas premissas e se termina na conclusão), estamos em condições de verificar se alguma vez ocorre aquilo que nenhum argumento válido permite, ou seja, se há alguma linha da sequência de tabelas em que as premissas sejam todas verdadeiras e a conclusão falsa. Se houver, ficamos a saber que o argumento ali representado não é válido, dado permitir que se parta de premissas verdadeiras para chegar a uma conclusão falsa. Mas se não houver, então o argumento é válido.
Pensemos no seguinte argumento:
O suspeito foi visto, no dia do crime, em Beja ou em Évora.
Ora, ele foi visto em Évora.
Logo, não foi visto em Beja.
Este argumento é válido ou inválido? Podemos fazer o teste de validade, construindo uma sequência de tabelas de verdade. Para isso, temos de começar por representar a forma lógica do argumento. Dado que ele é constituído pela combinação de duas proposições simples, começamos por estabelecer o seguinte dicionário:
P = O suspeito foi visto no dia do crime em Beja.
Q = O suspeito foi visto no dia do crime em Évora.
Com estas duas variáveis, obtemos a seguinte forma argumentativa:
P ⋁ Q
Q
∴ ¬P
|
P |
Q |
¬P |
P ⋁ Q, |
Q, |
∴¬P |
|
V |
V |
F |
V |
V |
F |
|
V |
F |
F |
V |
F |
F |
|
F |
V |
V |
V |
V |
V |
|
F |
F |
V |
F |
F |
V |
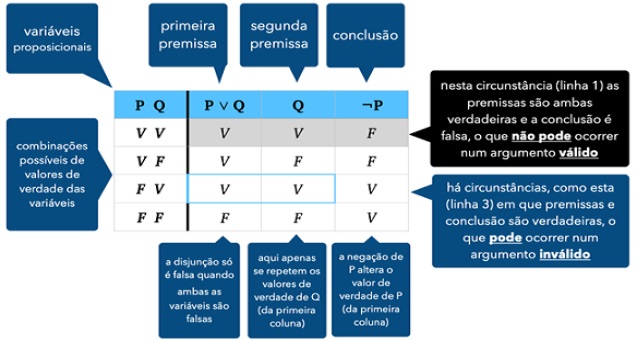
O sinal «∴» usa-se como indicador de conclusão. Assim, dado que temos três proposições (duas premissas e a conclusão), teremos também uma sequência de três tabelas, como se segue:
Uma vez construída a sequência de tabelas de verdade, estamos em condições de verificar se o argumento é válido ou inválido, bastando para isso interpretá-la corretamente. Isso significa inspecionar cada uma das circunstâncias, correspondentes a cada uma das linhas, procurando apenas uma coisa: premissas verdadeiras e conclusão falsa. É precisamente isso que não pode acontecer num argumento válido e é isso mesmo que encontramos logo na primeira linha. Não é sequer preciso continuar a inspecionar as restantes circunstâncias (ou linhas) para concluirmos que o argumento é inválido.
Assim, partindo daquelas premissas, não estamos logicamente autorizados a concluir que o suspeito não foi visto em Beja. É perfeitamente possível que ele tenha sido visto em Beja e em Évora no mesmo dia, pelo que a verdade das premissas não exclui a falsidade da conclusão, como a sequência de tabelas acima mostra.
E se o argumento fosse antes o seguinte?
O suspeito foi visto no dia do crime em Beja ou em Évora.
Ora, ele não foi visto em Évora.
Logo, foi visto em Beja.
Recorrendo ao mesmo dicionário, obtemos a seguinte forma argumentativa:
P ⋁ Q
¬Q
∴ P
Prestando alguma atenção, verificamos que este argumento tem a forma de um silogismo disjuntivo, uma forma de inferência válida. Mas também podemos confirmar que se trata de uma forma válida recorrendo ao teste das tabelas de verdade:
Este teste mostra-nos que, esta forma argumentativa, nunca permite ir de premissas verdadeiras para conclusão falsa, pelo que o raciocínio em causa é válido e podemos confiar nele.
EM RESUMO:
- Podem usar-se sequências de tabelas de verdade (com as premissas e a conclusão lado a lado) para testar a validade de certos argumentos.
- Ao inspecionar cada uma das circunstâncias (cada uma das linhas) vemos se em alguma delas as premissas são verdadeiras e a conclusão é falsa.
- Se houver pelo menos uma circunstância em que as premissas são verdadeiras e a conclusão falsa, então o argumento é inválido, independentemente do que acontece nas outras linhas.
- Se nenhuma das circunstâncias (ou linhas) tiver premissas todas verdadeiras com conclusão falsa, então o argumento é válido, independentemente dos valores de verdade que ocorrerem nas outras linhas.




Sem comentários:
Enviar um comentário